
Jan Nagler
Frankfurt School of Finance & ManagementProfessor in the Centre for Human and Machine Intelligence and
Head of the Deep Dynamics Group
Jan Nagler's research includes the understanding and control of networked stochastic systems, with applications at the interface between physics, biology, and socioeconomic systems, ergodicity breaking and risk and survival in uncertain environments. He is the Head of the Deep Dynamics Group, which aims for a deep understanding of real-world system dynamics in finance, economics, ecology, physics and socio-technological systems, in particular networks and networked socio-economic systems. The group tackles problems by combining cross-disciplinary explanatory (based on deep fundamental underlying mechanisms and principles) and predictive modelling (prediction using deep learning), while being deeply committed to an ethically aligned design of systems, in particular explanatory and socially responsible AI.
NETWORK & DATA
Identifying crises through network connections
Universality is a principle that fundamentally underlies many phenomena, ranging from epidemic spreading to the breakdown of global connectivity in networks. We evaluated large amounts of data and simulated the emergence and decay of various networks and discovered a generally applicable, universal law that explains small and large-scale network disruptions, relevant in communication, trade and social networks.
Fan, Meng, Liu, Saberi, Kurths, Nagler, Nature Phys. 16: 455 (2020)
NETWORK SCIENCE
Propagation patterns unravelled
From disease proliferation to cell functioning, spreading dynamics on networks impact many collective phenomena. The joint contributions of the interaction structure and local dynamics have now been disentangled, revealing three distinct types of spreading pattern, relevant in communication, biochemical and social networks.
Timme, Nagler, Nature Phys. 15: 308 (2019), feature for Hens et al., ibid., p.403.
SOCIOECONOMIC NETWORKS
How micro-level decisions impact large-scale structure
We studied how large-scale connectivity emerges from decisions made by rational agents who minimize their costs in trade networks. We analyzed how locally optimal decisions on the micro-level determine the network structure on the macroscopic scale, relevant in socioeconomic networks such as the World Trade Network.
Schröder, Nagler, Timme, Witthaut, Phys. Rev. Lett. 120, 248302 (2018)

EVOLUTIONARY DYNAMICS & GAME THEORY
Unexpected coexistence and reversed natural selection
Payoffs in evolutionary games may change over time. We studied the impact of temporally varying payoffs on the population dynamics. Even in equilibrium, two coexisting strategies may persistently receive different payoffs. This mechanism can induce unexpected effects such as anomalous coexistence of cooperators and defectors in the Prisoner's Dilemma, and a reversal of natural selection in other games.
Stollmeier, Nagler, Phys. Rev. Lett. 120: 058101 (2018).

COMPUTATIONAL SOCIAL SCIENCE
Complex contagion dynamics comes in three flavors
We end a long-standing debate on the universality classes of complex contagion dynamics, where infections or adoptions of ideas may spread only if susceptible individuals have multiple contacts to infected individuals within a short period of time.
Böttcher, Nagler, Herrmann, Phys. Rev. Lett. 118: 088301 (2017).
SOCIOECONOMIC NETWORK & DATA SCIENCE
Transport networks explained
Many transport networks such as the world aviation and trade network exhibit a highly interconnected core but also a periphery that frays into a loop-free tree. Modeling the balance between connectivity and profit explains such core-peripheries.
Verma, Russmann, Araujo, Nagler, Herrmann, Nature Commun. 7: 10441 (2016)
NETWORK SCIENCE
Explosive percolation
Review on explosive percolation, the sudden emergence of large-scale connectivity that results from repeated, small control interventions, relevant in physical and social networks.
D’Souza, Nagler, Nature Phys. 11: 531 (2015).

NETWORK & DATA SCIENCE
Possible origin of stagnation and variability of Earth's biodiversity
According to the fossil record, about 500 million years ago the number of marine species began growing exponentially and then leveled off for 200 million years before exploding again. To understand how and why these changes occurred, we have constructed a model of species dependence and analyzed fossil records.
Stollmeier, Geisel, Nagler, Phys. Rev. Lett. 112: 228101 (2014).

UNIVERSAL STATISTICS
Crackling noise
We show that when drops or dust particles coalesce, they often follow the same statistical laws as the noise made by crumpling paper, or the crackling noise from fireplaces. A closer look at ferromagnets help establish the conceptual link between the different phenomena.
Schröder, Rabari, Nagler, Nature Commun. 3: 2222 (2013).
NETWORK SCIENCE
Competing connections
How a complex network is connected crucially impacts its dynamics and function. We explain how single links may drastically change macroscopic connectivity in growing networks where new connections compete for addition.
Nagler, Levina, Timme, Nature Phys. 7: 265 (2011).

NEUROSCIENCE & STATISTICS
Scaling laws of being off
Human musical rhythms performed by laypersons and professional musicians follow scaling laws
that help to humanize computer-generated music.
Hennig et al., PLoS ONE 6, e26457 (2011); featured in Science, Nature Phys. and Nature.

NONLINEAR DYNAMICS
How random are dice?
Gamblers — and Einstein — have assumed that throwing a die gives a random result. But does it? Jan Nagler [...] and Peter Richter [...] have simplified the throw of a die [...]. The researchers calculated the dynamics and find that these are only truly chaotic, leading to complete randomness, for certain initial conditions.
Quote as featured in Nature 455: 434 (2008).
PUBLICATIONS
Ji, P., Wang, Y., Peron, T., Li, C., Nagler, J., Du, J., 2023. Structure and function in artificial, zebrafish and human neural networks, Physics of Life Reviews Vol. 45, pp. 74-111.
Luo, Z., Chen, W., Nagler, J., 2023. Universality of explosive percolation under product and sum rule, Physical Review E Vol. 108(3, Art. 034108).
Bao, X., Hu, Q., Ji, P., Lin, W., Kurths, J., Nagler, J., 2022. Impact of basic network motifs on the collective response to perturbations, Nature Communications Vol. 13(Art. 5301).
Böttcher, L., Nagler, J., 2021. Decisive conditions for strategic vaccination against SARS-CoV-2, Chaos: An Interdisciplinary Journal of Nonlinear Science Vol. 31(Article-No. 101105).
Fan, Meng, Liu, Saberi, Kurths, Nagler, Universal gap scaling in percolation, Nature Phys. 16: 455 (2020).
D'Souza, R., Gómez-Gardeñes, J., Nagler, J., Arenas, A. Explosive phenomena in complex networks, Adv. in Phys. 68(3):123-223 (2019).
Timme, M., Nagler, J. Propagation patterns unravelled, Nature Phys., Vol. 15, pp. 308-309 (2019).
Short summary: This is an invited News & Views article on “Spatiotemporal signal propagation in complex networks” by Hens et al., ibid., p.403.
Zotos, E., Nagler, J. On the classification of orbits in the three-dimensional Copenhagen problem with oblate primaries, Intern. J. Non-Linear Mechanics Vol. 108, pp. 55-71 (2019).
EE Zotos, FL Dubeibe, J. Nagler, E Tejeda, Orbit classification in a pseudo-Newtonian Copenhagen problem with Schwarzschild-like primaries, Monthly Notices of the Royal Astronomical Society 487(2): 2340-2353 (2019).
Nagler, J., Stollmeier, F. Long-Term Behavior in Evolutionary Dynamics from Ergodicity Breaking, in: Complex Networks X: Proceedings of the 10th Conference on Complex Networks CompleNet 2019, Cham: Springer, pp. 85-95 (2019).
Zimmer, P., Kruse, K., Nagler, J. Anomalous percolation features in molecular evolution, Phys. Rev. E Vol. 98(2) (2018)
Schröder, M., Nagler, J., Timme, M., Witthaut, D. Hysteretic percolation from locally optimal individual decisions, Phys. Rev. Lett.120(24) (2018)
F. Stollmeier, J. Nagler, Unfair and anomalous evolutionary dynamics from fluctuating payoffs, Phys. Rev. Lett. 120: 058101 (2018).
M. Schröder, N.A.M. Araújo, D. Sornette, J. Nagler, Controlling percolation with limited resources, Phys. Rev. E 96: 062302 (2017).
L. Böttcher, J. Nagler, H.J. Herrmann, Critical behaviors in contagion dynamics, Phys. Rev. Lett. 118: 088301 (2017).
L. Böttcher, M. Lukovic, J. Nagler, S. Havlin, H.J. Herrmann, Failure and recovery in dynamical networks, Sci. Rep. 7: 41729 (2017).
Y.S. Cho, M.G. Mazza, B. Kahng, J. Nagler, Genuine non-self-averaging and ultra-slow convergence in gelation, Phys. Rev. E 94:022602 (2016).
M.A. Böttcher, J. Nagler, Promotion of cooperation by selective group extinction, New J. Phys. 18: 063008 (2016).
M. Schröder, S. Chakraborty, D. Witthaut, J. Nagler, M. Timme, Interaction Control to Synchronize Non-synchronizable Networks, Sci. Rep. 6: 37142 (2016).
T. Verma, N.A.M. Araujo, J. Nagler, J.S. Andrade Jr. and H.J. Herrmann, Model for the growth of the World Airline Network, Int. J. Mod. Phys. C 27(12): 1650141 (2016).
M. Schröder, W. Chen, J. Nagler, Discrete scale invariance in supercritical percolation, New J. Phys. 18: 013042 (2016).
L. Böttcher, N. A. M. Araújo, J. Nagler, J. F. F. Mendes, D. Helbing, H. J. Herrmann, Gender Gap in the ERASMUS Mobility Program, PLoS One 11(2):e0149514 (2016).
T. Verma, F. Russmann, N.A.M Araujo, J. Nagler, H. J. Herrmann, Emergence of core-peripheries in networks, Nature Comm. 7: 10441 (2016).
A. A. Saberi, S. H. Ebrahimnazhad Rahbari, H. Dashti-Naserabadi, A. Abbasi, Y. S. Cho, J. Nagler, Universality in boundary domain growth by sudden bridging, Sci. Rep. 6: 21110 (2016).
R. D’Souza and J. Nagler, Anomalous critical and supercritical phenomena in explosive percolation, Nature Physics, 11: 531 (2015); cover Nature Physics (July 2015). Short summary: An invited Nature Physics Review on recently discovered anomalous behaviors in disordered systems, in particular in competitive percolation.
F. Stollmeier, T. Geisel, J. Nagler, Possible Origin of Stagnation and Variability of Earth's Biodiversity, Phys. Rev. Lett. 112: 228101 (2014); accompanied by a Max-Planck-Society press release and media coverage (including Editor’s). Short summary: A simple species interdependence network model explains how marine biodiversity could have grown and then leveled off, and why there is a difference to the growth of Earth’s continental biodiversity.
D. Lamouroux, J. Nagler, T. Geisel, S. Eule, Paradoxical effects of coupling infectious livestock populations and imposing transport restrictions, Proc. R. Soc. B (London): 2015282, 20142805 (2014), accompanied with an MPI DS press release.
W. Chen, M. Schröder, R. M. D'Souza, D. Sornette, J. Nagler, Micro-transition Cascades to Percolation, Phys. Rev. Lett. 112: 155701 (2014)
K. Zhu, W. Li, X. Fu, J. Nagler, How do online social networks grow? PLoS One, 9(6):e100023 (2014).
W. Chen, X. Cheng, Z. Zheng, N.N. Chung, R.M. D'Souza, J. Nagler, Unstable supercritical discontinuous percolation transitions, Phys. Rev. E 88: 042152 (2013).
M. Schröder, H.E. Rabari, and J. Nagler, Crackling noise in fractional percolation, Nature Commun. 3: 2222 (2013); accompanied by media coverage. Short summary: When drops or dust particles coalesce, they often follow the same statistical laws as the noise made by crumpling paper, or the crackling noise in ferromagnets.
W. Chen, J. Nagler, X. Cheng, X. Jin, H. Shen, Z. Zheng, and R. M. D'Souza, Phase transitions in supercritical explosive percolation, Phys. Rev. E 87: 052130 (2013).
D. Lamouroux, S. Eule, T. Geisel, J. Nagler, Discriminating the effects of spatial extent and population size in cyclic competition among species, Phys. Rev. E 86: 021911 (2012).
J. Nagler, T. Tiessen, H.W. Gutch, Continuous percolation with discontinuities, Phys. Rev. X 2: 031009 (2012); accompanied by media coverage. Short summary: Competition in percolation does not necessarily lead to globally continuous percolation processes (in contrast to the take-home in Science 333: 322, 2012).
S. Uppaluri, J. Nagler, E. Stellamanns, N. Heddergott, S. Herminghaus, and T. Pfohl, Impact of Microscopic Motility on the Swimming Behavior of Parasites: Straighter Trypanosomes are More Directional, PLoS Comput. Biol. 7(6): e1002058 (2011); accompanied by media coverage.
J. Nagler, A. Levina, M. Timme, Impact of single links in competitive percolation, Nature Physics 7: 265-270 (2011); accompanied by media coverage. Short summary: Adding competitively single links in complex networks can have dramatic effects on the network’s critical behaviors.
H. Hennig, R. Fleischmann, A. Fredebohm, Y. Hagmayer, J. Nagler, A. Witt, F. Theis, T. Geisel, The nature and perception of fluctuations in human musical rhythms, PLoS One 6: e26457 (2011); featured in Nature 479: 153 (2011); featured in Nature Physics 7: 930 (2011); featured in Science 334: 1183 (2011); Short summary: Human musical rhythms performed by laypersons or professionals follow scaling-laws that help to humanize computer-generated music.
J. Nagler, P.H. Richter, Simple model for dice loading, New J. Phys. 12: 033016 (2010).
J. Nagler, P.H. Richter, How random is dice tossing? Phys. Rev. E 78: 036207 (2008); featured in Nature 455: 434 (2008).
J. Nagler, M. Linke, M. Krieger, J. Schönke, and J. Wiersig, Leaking Billiards, Phys. Rev. E 75: 046204 (2007).
J. Nagler, J.C. Claussen, 1/f^alpha spectra in elementary cellular automata and fractal signals, Phys. Rev. E 71: 067103 (2005).
J. Nagler, Directed and undirected multiurn models in a one-dimensional ring, Phys. Rev. E 72: 056129 (2005).
J. Nagler, Crash test for the restricted three-body problem, Phys. Rev. E 71: 026227 (2005).
C. Hauert, J. Nagler, H.G. Schuster, Of dogs and fleas: How N uncoupled two state systems behave, J. Stat. Phys. 116: 1453-1469 (2004).
J. Nagler, Crash test for the Copenhagen problem, Phys. Rev. E 69: 066218 (2004).
J.C. Claussen, J. Nagler, and H.G. Schuster, Sierpinski signal generates 1/f^alpha spectra, Phys. Rev. E 70: 032101 (2004).
J. Nagler, C. Hauert, and H.G. Schuster, Self-organized criticality in a nutshell, Phys. Rev. E 60: 2706 (1999).
 BOOK CHAPTERS
BOOK CHAPTERS
Nagler, J., Hoven, J., Helbing, D. An Extension of Asimov´s Robotics Laws, in: Dirk Helbing (ed): Towards Digital Enlightenment, Cham: Springer, pp. 41-46 (2018).
X. Chen, J. Nagler, X. Fu, Information dissemination in social-featured opportunistic networks. In: Social Network Analysis: Interdisciplinary Approaches and Case Studies 10(15):309-342, CRC Press (2017).
K. Zhu, X. Fu, W. Li, S. Lu, J. Nagler, Population growth in online social networks. In: Social Network Analysis: Interdisciplinary Approaches and Case Studies 10(15):285-306, CRC Press (2017).
M. Timme, J. Nagler, Network Dynamics: Growth, Risk, Design and Control - Mathematical Concepts for “intelligent” self-organizing processes in Nature and Technology. In: Yearbook 2014 of the Max Planck Society.
J. Nagler, P.H. Richter, How does God play dice? In Reviews of Nonlinear Dynamics and Complexity: Volume 3 (2010), Ed. H. G. Schuster, VCH Wiley.
PODCAST
Podcast #1: Trevor Pinch
Podcast with Trevor Pinch about crashing planes, macho bikes, psychedelic music, synthesizers, transcontinental cables, solar neutrinos, social constructivism, self-driving cars and the limits of artificial intelligence, including appearances ranging from John Cage to Elon Musk.
Podcast #2, Part1: Ernesto Estrada
Amazing Cuba, Spanish table dancing, intercropping, drugs against fungi and bacteria, ribosomes and proteins, little plant killers (aka aphids), semiochemicals, fractional diffusion and calculus, population growth.
Podcast #2, Part2: Ernesto Estrada
Drug discovery and multiorgan damage in Covid-19: Biochemistry, potential drugs and pharmaceutical targets.
Podcast #2, Part3: Ernesto Estrada
Social balance, conflicts, wars and tribes. How do triangles help analyze Hollywood and Netflix divorces? Linear Algebra and Network science!
Minipodcast with Yannik Suhre
Minipodcast: Yannik Suhre
Conversation helpful for Frankfurt School students and colleagues: Easy Cloud Computing for everyone.
Watch the podcasts on Youtube and give your thumb up, share with others, write a comment or subscribe to my channel. Enjoy.
MEDIA
Frankfurt School of Finance & Management + Potsdam Institute for Climate Impact (2020), available here
Editor’s suggestion for Phys. Rev. Lett. 112: 228101 (2014), available here
Various features and interviews in newspapers including Süddeutsche Zeitung, Göttinger Tageblatt, Der Standard (Austrian national daily newspaper), Laborpraxis and Harvard Gazette, available here
Permanent feature article on How random is dice tossing? In Welt der Physik (German, 2012), available here
Radio podcast by T. Pinch & M. Lane on Zipf’s law (2012), available here
Features in scientific journals:
Physics Today (cover July 3rd, 2012)
Spektrum der Wissenschaften (2012)
Nature Physics 7: 930 (2011); Science 334: 1183 (2011); Nature 479: 153 (2011)
Nature 455: 434 (2008)
German radio features including NDR Info, NDR Kultur, Radio Eins, Göttinger Stadtradio & PI Radio (2011-2012).
6 Max Planck Society / MPI DS Press Releases (2011-2015)
Wired, New Laws Explain Why Fast-Growing Networks Break (2015), available here
Online media coverage includes dradio, innovations-report, idw-online, ahano, strategie news, extremnews, science one, scinexx, chemie.de, physorg and other online services (2011-2015)
Projects
[network + data science]

Please find part of a press release of the most recent publication [Fan, Meng, Liu, Saberi, Kurths, Nagler, Universal gap scaling in percolation, Nature Phys. 16: 455, 2020]:
>>Jan Nagler (…) led a team of researchers to explain the emergence and collapse of large networks. Their study was published on 20 February in Nature Physics. The international research team, which also includes scientists from the Potsdam Institute for Climate Impact Research, evaluated large amounts of data and simulated the emergence and decay of various networks. In doing so, they discovered a generally applicable law that explains the largest network disruptions. For example, a perfectly functioning network of proteins in our cells generally correlates with the absence of diseases such as Alzheimer's. In a protein-protein-interaction network with thousands of proteins and known interactions, the scientists were able to show how accumulated disturbances in a few interactions affects the entire network.
"We have developed a mathematical model that describes the probability of global collapse, regardless of the details of the particular network," said Dr Jingfang Fan from the Potsdam Institute for Climate Impact Research and first author of the study. Professor Nagler adds: “Our research was helped by a concept from the financial world that quantifies extreme changes in fluctuating financial markets. We have shown that this concept also describes rapid growth or collapse of large-scale networks.”
In their interdisciplinary work, the scientists combined methods from finance, physics, biochemistry, engineering and social sciences, and were able to establish for the first time a conceptual link between small and large-scale network disruptions. In the future, the theory may help to rein in percolation with timely countermeasures - such as closing airports when an epidemic spreads.<<
The established universal framework for percolation will be used to estimate the risk of large-scale breakdowns, given only a few network snapshots. Specifically, the universality of extreme value theory applied to networks will help my group devise an early-warning method for future crises in networked socio-economic systems and ecosystems. The combination with other early-warning signals, in particular, appears promising.
[network + economic sciences + machine learning]

We are living in a networked world. Almost all pressing techno-socio-economic problems of our time (mass migration, traffic jams, growing megacities, climate change, biodiversity loss, public health) are related to networks. Thus, we cannot solve the problems without attacking those from a network perspective. Building on fundamental principles from network science and machine learning (with well-chosen optimization objectives) may help to develop solutions that have appeared unfeasible for decades (Timme & Nagler, Propagation patterns unravelled, Nature Phys. 15: 308, 2019). In a number of projects, we will study the limits of optimization of ride-hailing due to hysteresis and other fundamental (network) effects. The pressing problem of congestion pricing may be even solved by a combination of fundamental principles, network science and computational methods. To demonstrate proof-of-concept and robustness, we will perform large-scale traffic ride-hailing simulations where also long-term business strategies of car fleets based on traffic forecast (similar to Waze or Uber) and congestion game theory are formulated and simulated.
[network + data science + machine learning + digitization]
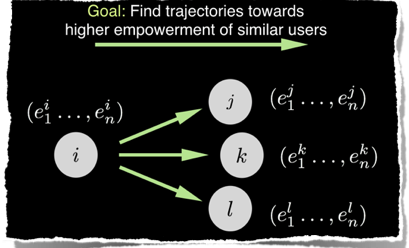
In essence, a (social or living) system that follows a homeokinetic principle would explore the environment in order to maximize the number of choices, or options, at a given time and for the future. For example, toddlers try to learn to stand up and master upright gait due to their homeokinetic desire to be able to better explore the environment. This evolutionary program of maximization of options can ensure survival (in fluctuating environments) and the development of intelligent (social or robotic) behaviors.
Can we build social networks that could give us a different perspective on our work life balance, or provide incentives in favor for, e.g., changing our (unhealthy) life style? The implementation of homeokinetic principles could guide us to escape through bottlenecks, away from recurrent personal behavioral patterns, to places where we want to be, to behaviors which are better for us. My group will combine machine learning and network science to translate homeokinetic principles to algorithms with the objective to evolve (online) social networks in ways that reflect our long-term goals and development. Building on research in homeokinetics in robotics [Der & Martius, PNAS: 112, E6224, 2015], we will develop algorithms that suggest new online social contacts. Can we better reorganize social networks in such a way that our community follows a collective homeokinesis? Can homeokinetic principles coexist with existing myopic attention-driven maximization objectives of “Facebook & Co”? How to use Big Data? And how not to use it? An ethically aligned design of data-driven human-centered homeokinetic networked systems lies at the heart of my most ambitious long-term scientific goals
[network + data science]

We showed when and how exactly environmental fluctuations can transform winning evolutionary strategies to losing ones, or vice versa (Stollmeier & Nagler, Unfair and anomalous evolutionary dynamics from fluctuating payoffs, Phys. Rev. Lett. 120: 058101, 2018). The fundamental mechanism behind this is called ergodicity breaking and can lead, e.g., to a reversal of natural selection. In complex ecosystems (Stollmeier, Geisel, Nagler, Possible Origin of Stagnation and Variability of Earth's Biodiversity, Phys. Rev. Lett. 112: 228101, 2014), both in theory and in ecological data, we will analyze the impact of ergodicity breaking on biodiversity on large and global scales. Since temperature fluctuations cause this effect, we will be able to predict the impact of temperature fluctuations from climate change on ecosystems.
In a number of collaborations, first experiments in vivo (in nematodes from La Reunion, M. Leaver) have shown that our theoretical prediction is exact. We could show that we can predict population growth from first principles, without fitting. We will develop a framework to predict biodiversity loss in networked ecological systems.
[machine learning]

Current reinforcement learning schemes typically generalize insufficiently. Changes of functionally irrelevant features such as the color of objects in Atari games may render a well-trained (DQN)network originally exhibiting super-human performance a losing algorithm. In a recent paper (Thomas et al., Preventing undesirable behavior of intelligent machines, Science 366: 999, 2019), the authors study a maximization objective subject to an additional constraint. Specifically, the performance must not fall below a certain accuracy at no time. A robosurgeon, e.g., must not make a single big mistake during a surgery, otherwise it would be useless, even if the average performance would be high.
Some birds may lose more than 20% of their body weight in a single winter night, if they cannot find food. Thus, in an evolutionary setting, to survive, the reward rate must be higher than a certain threshold. On the other hand, rewards cannot always accumulate forever. Squirrels may collect a large number of nuts to survive periods of scarcity but collecting nuts may be too energy-consuming and dangerous for other reasons, e.g., foraging may expose squirrels to predators.
Human evolution may be the main driving force of the emergence and long-term maintenance of human general intelligence. Taken together, we will develop reinforcement schemes based on a non-extremal reward objective that represents survival, formalized by using a critical threshold of the reward rate – but not reward maximization. In terms of economics, we impose a utility function with a constant tail (“minus reverse ReLU”, in CS jargon). With the choice of the proper loss function (objective), we will redesign reinforcement learning such that a deep neural network representation that ensures survival in an unpredictable fluctuating environment, as typical for life on not-too-small time scales, necessarily emerges. Depending on the time-scale of the environmental changes (training data), and their predictability and magnitude (covariance), rapid activity switching between learned modular structures may emerge: a generalist who avoids overfitting through long-term survival.

